Для построения имитационной модели формирования гранулометрического состава погружаемого материала в малом выделенном объёме V предлагается генерировать случайным образом число кусков каждого разряда в отдельном опыте. При этом может быть использован известный биноминальный закон распределения [97]:
, (2.1)
где х – дискретная случайная величина, которая может принимать возможные значения 0, 1, 2, …, n; Р(X = m) – вероятность того, что случайная величина X примет значение m; q = 1 – р – вероятность противоположного события; 
– число сочетаний из n элементов по m.
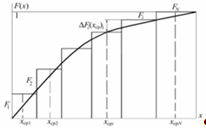
Рис. 2.3. Замена непрерывного распределения дискретным
Выделенный малый объём V заполняется кусками, представляющими по размерам дискретный ряд xcp1×dmax; xcp.2×dmax; …; xcp.N×dmax. Зная объём V, можно найти максимальное число кусков каждого разряда, которое может разместиться в этом объёме:
.
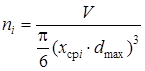Таким образом, моделируемая случайная переменная mi в каждом разряде изменяется в пределах 0; 1; 2; …; ni. Для построения дискретного распределения, подчиняющегося биноминальному закону, необходимо определить вероятность единичного события р – попадания куска i-й фракции в объём v. В работе показано, что вероятность р приближенно равна долевому участию по объёму кусков данного разряда 
i в общем объёме штабеля.
Теперь, по известным ni и i, можно построить биноминальный закон распределения вероятности выпадения числа кусков данного разряда mi в пределах от 0 до ni. На основе этого закона в каждом черпании можно с использованием генератора случайных чисел задавать случайное значение mi – число кусков i-го разряда, попавших в ковш, перед кромкой ковша, лапы, клина и т.д.
Проверка адекватности моделирования реальному гранулометрическому составу штабеля должна проводиться после k опытов (число k может быть установлено на основе распределения Стьюдента для малого объёма выборки). По каждому разряду среднее значение 
приближается к математическому ожиданию: mxi = ni i.
Другой проверкой адекватности раздельного моделирования заполнения ёмкости v как независимого числа кусков каждого разряда является выполнение условия:
.
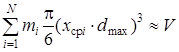Изменение гранулометрического состава исходного штабеля после очередного черпания производится в следующем порядке:
1) вычисляется суммарный объём выгруженного материала из штабеля после каждого j-го черпания:
;
2) находится остаточный объём штабеля после j-го черпания:
Vj = Vj-1 – VУ;
3) определяется новое долевое содержание каждой фракции i (xcpi) к началу (j+1)-го черпания:
.
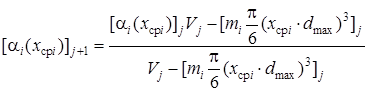Таким образом, формируется новый гранулометрический состав штабеля как функция [i (xcpi)]k, где k = 1, 2,….,j, j+1, … k, k – число черпаний ковшом из штабеля. Для каждого последующего состояния штабеля должно соблюдаться соотношение: