лебёдка подъёма ковша соединена с двигателем через функциональную муфту, включение которой производится оператором по некоторому закону. В результате постепенного нарастания момента включающей муфты скорости цепи на барабане и в точке крепления ковша выравниваются; в этом случае цепь может приниматься абсолютно жёсткой.
При составлении уравнений внешней динамики системы подъёма ковша необходимо учитывать следующие особенности:
а) момент сопротивления зачерпыванию Мз является функцией угла поворота ковша Мз = Мз(
к); максимальное значение Мз.max определяется по математическим моделям (3.24) – (3.26); величина к.max определяется характером траектории движения передней кромки ковша; функция Мз = = Мз(к) имеет два участка: 0 ≤ к ≤ к.max и к.max < к ≤ кпр (рис. 3.14);
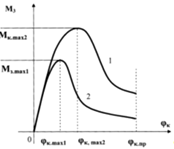
Рис. 3.14. Зависимость момента сопротивления черпанию Мз от угла поворота ковша к (1 – траектория «крутая»; 2 – траектория «пологая»)
б) систему «двигатель – редуктор – барабан – цепь – ковш – горная масса» можно рассматривать как двухмассовую; в каждую из групп масс необходимо вводить вращающиеся элементы, имеющие одинаковые или строго пропорциональные угловые скорости; для схемы с жёсткой кинематической связью (рис. 3.13а) вращающиеся массы разделяются следующим образом: Iоб – момент инерции ротора двигателя, передаточного редуктора и барабана с радиусом навивки цепи rб; IкУ – момент инерции ковша относительно собственной оси вращения в сумме с вращающимися массами сдвигаемого объёма захвата; для схемы с включающей функциональной муфтой (рис. 3.13б) вращающиеся массы разделяются также на ведущие – Iоб – ротор – часть редуктора до включающего фрикционного элемента и IкУ – ведомые – часть редуктора – барабан – ковш – горная масса;
в) момент инерции ведущей части динамической системы Idб может быть принят постоянным и с учётом известных допущений, определённых с помощью соотношения
Iоб = KJ × Iдв × 
, (3.35)
где Iдв – собственный момент инерции приведённого двигателя, кг×м2; iоб – передаточное число механизма от вала двигателя до ведущего элемента (в варианте а – до вала барабана, а в варианте б – до ведущего элемента фрикционной муфты); КJ – коэффициент, учитывающий влияние вращающихся масс редукторов, барабана и т.п. (КJ ≤ 1,1 [33]);
г) момент инерции ведомой части IкУ является величиной переменной; основными составляющими являются: момент инерции собственно ковша Iк моменту инерции сдвигаемого объёма захвата Iпор = Iпор (к); в процессе поворота ковша на угол 0 ≤ к ≤ к.кр меняется радиус инерции ковша ск(к), масса сдвигаемого объёма mпор(к) и радиус инерции этой массы спор (к); таким образом, для ведомой части системы момент инерции относительно центра вращения O может быть определён из следующего соотношения:
. (3.36)
Дифференциальные уравнения, описывающие движение системы при зачерпывании, имеют вид (вариант а):
для ведущей части системы:
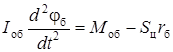; (3.37)
для ведомой части системы:
; (3.38)
усилие в цепи:
. (3.39)
В этих уравнениях дополнительно к ранее введённым обозначениям: l(к) – плечо силы тяжести ковша в процессе поворота, м; С – жёсткость цепи, Н/м; ∆lц – удлинение цепи, м.