Затем с помощью генератора rnorm (n, mA, sigA) [98] производилось формирование случайной выборки методом 2 с той же размерностью; над этой выборкой производились те же статистические процедуры.
Оценка степени соответствия массива 1 и 2 и их принадлежности одной генеральной совокупности производилась путём определения:
– оценки для ковариации, которая характеризует степень зависимости случайных величин HN(n) и A(n) и их рассеивание вокруг точки 
:
;
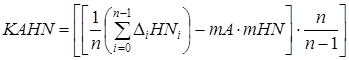– оценки для коэффициента корреляции случайных величин массивов A(n) и HN(n), характеризующих степень зависимости этих величин:
;
– границ доверительного интервала коэффициента корреляции при доверительной вероятности 95 %.
Обозначения величин соответствуют программе моделирования в среде MathCad: Ai; HNi – массивы 1 и 2; mA; mHN – математические ожидания выборок 1 и 2; n – размерность выборки; DA, DHN – дисперсии выборок 1 и 2; KAHN – оценка ковариации; RAHN – оценка коэффициента корреляции.
Результаты статистического сопоставления выборок, полученных методами 1 и 2, для различных F(d) и u представлены в таблице 2.9.
Как следует из результатов моделирования, распределение случайной величины dср.j подчиняется нормальному закону. Для всех функций F(d) и диапазона изменения малого выделенного объёма относительная ошибка от замены процедуры 1 процедурой 2 не превышает по математическому ожиданию 1,5 %, по среднеквадратическому отклонению – 6 %. Коэффициент корреляции связи массивов близок к единице.
Следовательно, средний размер куска dср.j при имитационном моделировании рабочих процессов ППТМ можно представить как случайную величину, распределённую по нормальному закону с параметрами:
математическое ожидание выборки равно математическому ожиданию размера кусков в штабеле;
среднеквадратическое отклонение и коэффициент вариации являются функциями среднего относительного размера куска и величины малого выделенного объёма (рис. 2.8).
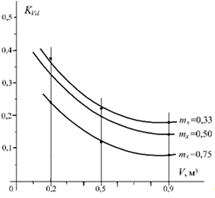
Рис. 2.8. Зависимость коэффициента вариации среднего случайного размера куска KV от гранулометрического состава (mx) штабеля и величины малого выделенного объёма v
Для конкретных условий величину коэффициента вариации среднего случайного размера куска в объёме можно найти по формуле:
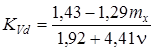, (2.3)
где 
; 
; 
– средний размер куска в штабеле, м;
dmax – максимальный размер куска в штабеле; sd – среднеквадратическое отклонение случайной величины среднего размера куска в малом объёме 
.
Формула (2.3) получена методом наименьших квадратов, максимальная ошибка не превышает 7,5 %. Таким образом, упрощённый порядок моделирования среднего случайного размера куска 
в малом выделенном объёме 
сводится к следующему:
в качестве исходных данных используется гранулометрический состав штабеля Fi (x), i = 1; 2; 3; 4; 5, для которого известен средний относительный размер куска 0,25 £ mx £ 0,75 (см. п. 2.2);