Имитационные процедуры, описанные в п. 2.3, обеспечивают получение dср.j в заданном объёме v. Однако разработанный метод отличается громоздкостью: для каждой j-й реализации черпания ковшом или нагребающей лапой необходимо поразрядно «комплектовать» объём v целым количеством кусков ni согласно биномиальному закону распределения; затем определять фактический случайный объём материала внутри «ёмкости» v, производить корректировку и определять dср.j; далее, после очередного черпания изменять гранулометрический состав штабеля F(d) и повторять цикл вычислений.
Рассмотрим возможности упрощения описанной процедуры на основе гипотезы о нормальном распределении среднего размера куска в малом выделенном объёме v, если v << Vшт. Будем считать, что 
– случайная величина, распределение по нормальному закону с параметрами dср.F и sср.F, где dср.F – математическое ожидание размера куска в штабеле с функцией распределения F(d); sср.F – среднеквадратическое отклонение случайной величины dср.j; j = 
такие для горной массы с функцией распределения F(d).
На рисунке 2.7 представлены для сравнения гистограммы и плотности вероятности распределения кусков среднего размера для штабелей F4(d) (рис. 2.7а) и F3(d) (рис. 2.7б). В каждой из реализаций совокупность случайных значений dср.j получена: – с использованием ступенчатой процедуры через формирование объёма n на основе биномиального распределения, – прямым моделированием на основе нормального распределения (N – число черпаний, ni – число значений в данном разряде).
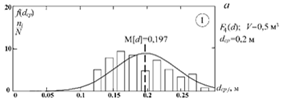
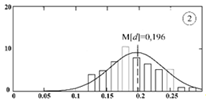
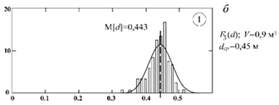
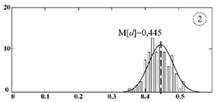
Рис. 2.7. Сравнение распределений dср.j исходным методом на основе биномиального распределения (1) и прямого моделирования на основе нормального распределения (2)
Как видно из визуального сопоставления гистограмм 1 и 2 и плотностей распределения f(dср.), прямое моделирование с использованием нормального закона распределения представляется вполне оправданным. Для статистической оценки возможности замены процедуры 1 на процедуру 2 для диапазона изменений функций F(d) – от F3(d) до F4(d) и для малых выделенных объёмов 
= 0,2; 0,5; 0,9 м3 выполнено статистическое моделирование в среде MathCad и оценка гипотезы возможной замены процедур.
Для каждой выборки dср.j(Ai), полученной с использованием процедуры 1, после ввода массива размерностью N(n) проводилась сортировка по возрастанию значений dср.j(Ai), вычислялось математическое ожидание mA(
), ошибка в отклонении mA от генерального среднего, несмещённая оценка дисперсии DA и среднеквадратического отклонения sigA. Затем выполнялось построение гистограммы, для чего устанавливались минимальное и максимальное значения dj.min (xmin) и dj.max (xmax); принималось число интервалов разбиения m и размер интервала (dmax – dmin)/mj, определялось число значений dср.j, попадающих в данный интервал; далее производилось построение гистограммы для выборки 1.