В методе конечных элементов (МКЭ) сплошное тело, имеющее бесконечное число степеней свободы, разбивают на элементы ограниченной протяженности и, используя характеристики отдельных элементов, описывают поведение системы в целом.
Метод конечных элементов получил значительное развитие с 1950-х годов, когда появились большие ЭВМ. В настоящее время этот метод находит широкое применение при решении различных технических задач, к которым можно отнести задачи сопротивления материалов, гидромеханики, теплотехники, электротехники и др. При рассмотрении конечных элементов используются различные методы: метод перемещений, метод напряжений, комбинированный метод и т. д. При исследовании механизма поведения композитов методом конечных элементов обычно ограничиваются анализом двумерной задачи [15].
При решении двумерных плоских задач методом конечных элементов прежде всего необходимо рассматриваемую область (рисунок 3.1) разбить на конечные элементы. Вершины элементов носят названия узлов. Выберем на рисунке 3.1 для рассмотрения какой-либо элемент (рисунок 3.2). На этот элемент действуют внешние силы Xν и Yν, под действием которых происходит деформация элемента, рассматриваемого как упругое тело. В данном случае можно соответствующим образом установить узлы конечных элементов и определить усилия, действующие в узлах, полагая, что внешние силы, действующие на элементы, передаются лишь через узлы. Форма элементов, на которые разбивают тело, может быть самой разнообразной. Часто используют элементы треугольной формы, три вершины которых выбираются в качестве узлов (рисунок 3.3)
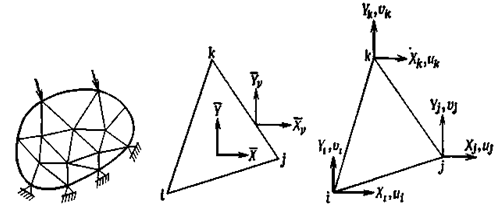
Рисунок 3.1 – Аппроксимация конечными элементами
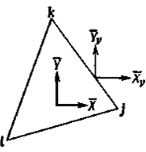
Рисунок 3.2 – Конечный элемент
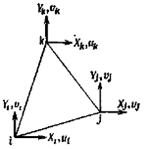
Рисунок 3.3 – Треугольный элемент
В общем случае изменение формы внутри элементов, на которые разбито непрерывное тело, носит сложный характер. Это обстоятельство вынуждает ввести допущение о том, что перемещения внутри элементов являются простыми. В таком случае на основании использования перемещений узлов элемента {δ} можно определить перемещения и и v в произвольной точке (х, у) рассматриваемого элемента
![]()
где величины u и v, характеризующие перемещения, полученные с учетом введенного допущения, носят название функций перемещения, а матрица [N] называется матрицей формы [15].
Для МКЭ характерно:
– широкий диапазон применения;
– инвариантность по отношению к конструкции и механическим характеристикам материала;
– простота учета взаимодействия конструкции с внешней средой.
Основные этапы расчета конструкции по МКЭ:
1) Разбиение рассматриваемой конструкции на конечные элементы и подготовка топологической, геометрической и физической информации, а также установление факторов взаимодействия с окружающей средой;
2) Построение для выделенных конечных элементов соответствующих матриц – жесткости, напряжения – деформации, деформаций – перемещений, а также векторов, определяющих зависимости между реакциями и перемещениями в узлах элемента;
3) Формирование разрешающей системы линейных алгебраических и дифференциально-алгебраических уравнений;
4) Решение полученных систем;
5) Обработка результатов и анализ работы конструкции [15].
Для треугольного элемента, представленного на рисунке 3.3, воспользуемся следующим допущением, согласно которому, прямая линия, соединяющая две произвольные точки в элементе, остается прямой линией после того, как элемент изменит свою форму [15].
