Все свойства и параметры самолёта между собой взаимосвязаны. Математическим отображением этой взаимосвязи является уравнение баланса масс самолёта.
;
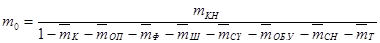где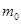 
- взлётная масса самолёта.
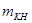- масса коммерческой нагрузки.
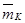- относительная масса крыла.
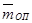- относительная масса оперения.
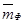- относительная масса фюзеляжа.
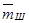- относительная масса шасси.
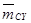- силовой установки.
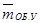- оборудования и управления.
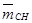- снаряжения.
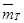- топлива.
Выбор и обоснование метода организации технологического
процесса ТО и ТР
На выбор метода обслуживания влияют следующие факторы:
– сменная программа по ТО данного вида;
– характер объема и содержание работ по данному виду ТО (постоянный или переменный);
– количество и тип подвижного состава;
– число рабочих постов для ТО данного вида;
– период времени, отводимый на обслуживание данного вида;
– трудоемкость обслуживания;
– режим работы автомобилей по линии.
Необходимыми условиями проведения ТО на поточной лини ...
Подбор и расчет необходимого оборудования колесотокарного отделения
Количество оборудования і-го типа колесно-токарного отделения рассчитывается по формуле:
(5.8)
где tі – расходы станко-часов на обработку колесной пары на станке і-го типа, в табл. 5.1
Количество оборудования для механической очистки:
принимаем
Для другого оборудования и Боб1пр приведено табл. 5.1.
Расчетное количество оборудования округляется к большему целому числу Бобипр, в связи с этим вводится коэффициент загрузки оборудования.
...
Нагрузки, действующие на лопасть и лонжерон
В полете лопасти нагружаются воздушными и массовыми (инерционными) силами. Для упрощения представления о распределении нагрузок их можно разделить на две группы:
1 Нагрузки, действующие в плоскости наименьшей жесткости лопасти в плоскости взмаха (рисунок 1.12, а). К ним относятся: воздушная нагрузка Y в; нагрузка от веса конструкции лопасти Y к; центробежная сила Nцб а также инерционная сила Y β от углового ускорения при маховом движении ...