Страница 2
F(0) = 0; F = (1) = 1;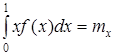 
,
где 
; 
.
Наряду с аппроксимацией гранулометрического состава рядового штабеля по экспериментальным данным при mx4=0,33, построены функции распределения крупности кусков «прогнозных» штабелей (рис. 2.2), в которых сохраняются или имеют симметричный вид функции распределения, но различаются средними размерами куска: mx1=0,5; mx2=0,67; mx3=0,75; mx5=0,25. Кривые F4(x) и F5(x) имеют экспоненциальный закон распределения, линия F1(x) – закон равномерной плотности F1(x) = x; кривые F2(x) и F3(x) построены как симметричные относительно линии F1(x) соответственно законам распределения F4(x) и F5(x):
.
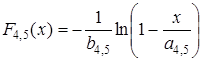Таким образом, получено математическое описание гранулометриче-ского состава штабелей в широком диапазоне изменения среднего размера куска (0,25…0,75) dmax. Это позволяет исследовать влияние состава штабе-ля по крупности на показатели работы погрузочно-транспортных модулей.
Анализ продолжительности обслуживания судна
Qф = 1,05*11260 = 11823т;
Рф = 1,1*20,94 =23,03 т/ч;
nф = 1,15*4 = 4,6;
Uф=0,9*1 = 0,9.
Сф = 1,05*52,09 =54,69 грн
ТТф =
11823
=124,01 ч.
23,03*4,6*0,9
ТТп =
11260
=134,43 ч.
20,94*4*1
Таблица №11. Анализ результатов ПОС.
Показатели
Обозначе-ния
Значения
Отклонения (Δ)
план
факт
Загрузка судна, т
Q
11260
11823
-563
Производительность ТЛ, т/ч
P ...
Мероприятия по ТБ
Рабочие, занятые ремонтом аккумуляторных батарей и их обслуживанием, постоянно имеют контакты с вредными веществами (пары свинца, серной кислоты), которые, при определенных условиях или неправильном обращении, могут привести к травме или отравлению организма. Кроме того, при зарядке АКБ происходит химическая реакция, в результате которой смешиваются выделившийся свободный водород с кислородом в любых пропорциях и образуется летучий газ, взрываю ...
Затраты на смазочные материалы
Расход смазочных материалов определяется исходя из установленных норм на 100 л расхода топлива для каждого вида смазки.
Расход смазочных материалов определятся по следующей формуле для каждого вида материала:
где Нсмi - норма расхода i-го вида смазочного материала на 100л топлива,
Цсмi - цена i-го вида смазочного материала на 100л топлива.
1 кругорейс: EUR
2 кругорейс: EUR ...
