Описание состава штабеля как функции случайной величины размера куска

В настоящее время традиционно состав штабеля по крупности слагающих его кусков di описывается с помощью приближённой гистограммы распределения, в которой указываются диапазоны разрядов идолевое содержание объёмов фракций. Например, так называемый рядовой штабель [44] имеет разряды (в м) – 0–0,1; 0,1–0,2; 0,2–0,4; 0,4–0,6 и соответствующее процентное содержание – 30; 30; 30; 10 (рис. 2.2). С помощью гистограммы можно определить средний размер куска dср в полном объёме штабеля. Такое представление состава штабеля недостаточно информативно и не позволяет с достаточной точностью решать задачу о гранулометрическом составе малого объёма v << V, где V – объём штабеля и, соответственно, о среднем размере куска в объёме v. Это, в свою очередь, препятствует разработке математических моделей процессов взаимодействия погрузочных и транспортирующих органов со штабелем при случайном изменении размера куска.

Гранулометрический состав рядового штабеля

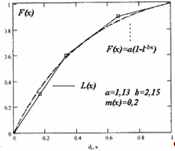
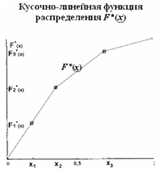
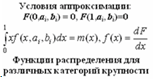
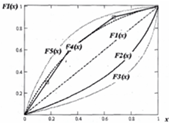
Рис. 2.2. Описание штабеля как функции случайной величины размера куска di

В реальном штабеле размер куска d – это непрерывная случайная величина, которая изменяется в пределах (0, dmax). Такое утверждение следует из того, что число кусков в штабеле достигает порядка 104. Поэтому состав штабеля логично представить в виде непрерывной функции F(d) (или плотности f(d)) распределения случайной величины d [93, 94].

Подбор аппроксимирующей кривой F(d) выполнен путём следующих преобразований экспериментальной гистограммы распределения (рис. 2.2):

в качестве случайной величины X выбрано отношение d/dmax, что позволило придать функции F(x) безразмерную форму;

по экспериментальным данным построена ступенчатая функция распределения , где – вероятность (частость) попадания случайной величины xn на соответствующий интервал;

через точки А1, А2, …, Аn проведена теоретическая функция распределения F(x), удовлетворяющая условиям 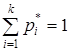; 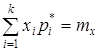, где mx – математическое ожидание случайной величины x = d/dmax;

соответствие теоретической функции распределения F(x) экспериментальным данным оценено с использованием критерия Пирсона – c2 [96].

По приведённой методике оценена степень приближения для ряда известных несимметричных функций распределения и показано, что наибольшей теснотой связи обладают логнормальное и экспоненциальное распределения. Последнее принято в качестве основного для дальнейших исследований. Функция распределения имеет вид: F(x) = a (1 – e –bx).

Значения коэффициентов a и b определялись в среде MathCad [98] по граничным условиям, заданной величине математического ожидания при минимальном среднеквадратическом отклонении искомой кривой от экспериментальных точек: